
소수를 판별하는데 자주 쓰이는 에라토스테네스의 체를 정리해보자. 벨로그에 정리했었지만 다시 한번 정리해보려고 한다.
소수(Prime number)란?
1보다 큰 자연수 중 1과 자기 자신만을 약수로 가지는 수를 소수라고 정의한다. 소수를 작은 순서대로 나열하면 2, 3, 5, 7, 11, 13, 17, 19, 23...이며 코딩테스트를 준비한다면 바로바로 생각할 수 있게 2, 3, 5, 7까진 외워두는 것이 좋다. 소인수분해(소수의 곱) 문제를 풀 때도 소수는 중요한 부분을 차지한다. 반대로 소수가 아닌 수는 합성수라고 한다.
에라토스테네스의 체(Sieve of Eratosthenes)
에라토스테네스의 체는 고대 그리스의 수학자인 에라토스테네스가 발견한 소수를 구하는 방법으로 2의 배수, 3의 배수 등을 체처럼 걸러내 소수만 남기는 방법이다. 어떤 1개의 수가 소수인지 아닌지 판별하는 방법은 여러가지 좋은 방법이 있지만, 이처럼 1부터 N까지 여러 개의 수 중에서 소수만을 빠르게 찾아내는 방법으로는 보통 이 에라토스테네스의 체를 이용한다.
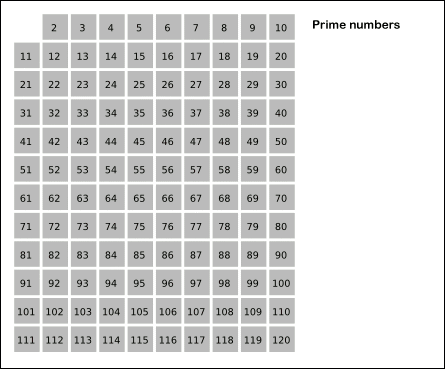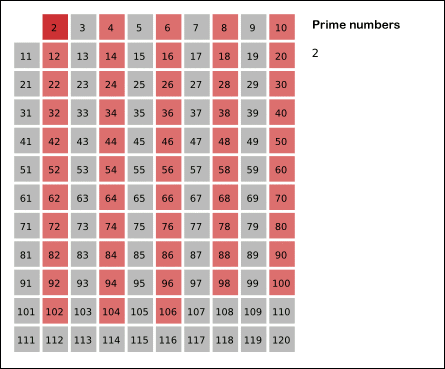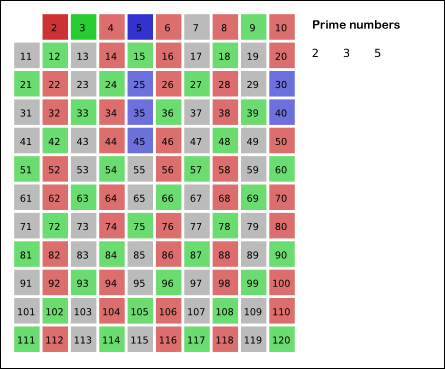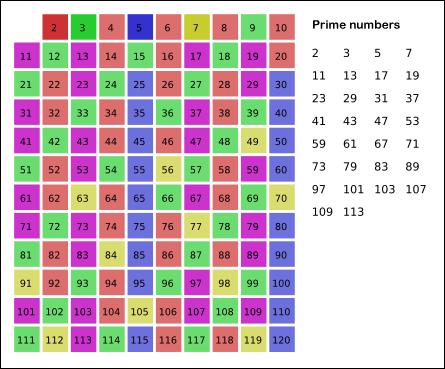
에라토스테네스의 체의 기본적인 개념은 위의 그림처럼 2의 배수, 3의 배수, 4의 배수, 5의 배수...를 차례대로 제거하는데 각 사이클마다 지워지지 않은 수 중에서 가장 작은 수를 소수로 채택한다.
1. 1을 제거. 남은 수 중에서 가장 작은 수가 2이므로 2를 소수로 채택
2. 소수로 채택된 2를 제외하고 2의 배수를 제거. 남은 수 중에서 가장 작은 3을 소수로 채택
3. 소수로 채택된 3을 제외하고 3의 배수를 제거. 남은 수 중에서 가장 작은 5를 소수로 채택
4. 소수로 채택된 5를 제외하고 5의 배수를 제거. 남은 수 중에서 가장 작은 7를 소수로 채택
.
.
.
제거하기
에라토스테네스의 체는 왜 배수로 제거를 할까? 우선 어떤 자연수 36이 소수인지 아닌지 판별하자

36은 2와 3으로 이루어진 합성수로 소수의 정의에 따라 소수가 아니다. 즉, 36은 2로 나눌 수 있기도 하고 3으로 나눌 수 있기도 하다. 따라서 어떤 값 n이 m, l, ...로 이루어진 수일 때 n을 m으로 나누면 나머지가 0이 된다. 이를 이용해 합성수를 제거할 수 있다.

1은 소수에 포함하지 않으므로 제외하고 2의 배수부터 제거해보자. 사실상 2를 제외한 짝수는 여기서 다 제거되므로 소수는 2를 제외하면 항상 홀수이다.

3의 배수를 제거해보자. 3은 소수이므로 제외하고 9, 15, 33이 있다.

3의 배수를 제거하고 이제 4의 배수를 제거할 차례인데 이미 4의 배수 8, 12, 16, 20 등은 2의 배수를 제거할 때 전부 제거 됐다. 즉, 이미 제거된 수의 배수들은 제거할 필요가 없다. 이런 식으로 계속해서 반복하면 남아 있는 값들이 소수가 된다.
이제 또 하나의 궁금증이 생긴다. 만약 100만개의 수가 있을 때 위와 같이 2의 배수, 3의 배수 등으로 초반에 대부분 제거하고 나면 후반부로 갈 수록 남은 수가 더 드문드문 있을텐데 이 소수들을 찾기 위해 1,000,000까지 다 체크해야 할까? 대체 어느 배수까지 제거해야 소수만 남을까?
제곱근
1부터 N까지의 수 중에 소수를 판별해야 한다고 하자. 1~N 사이의 어떤 값 X는 위의 그림에서 봤듯이 A x B라고 할 수 있다. 즉, X가 17이라면 1 x 17, 20이라면 4 x 5이다. 여기서 X의 부분인 A, B중에 적어도 하나는 N의 제곱근보다 작거나 같다.

무슨 말이냐 하면 만약 X의 부분인 A와 B가 둘다 N의 제곱근보다 크다면 무조건 X는 N보다 커진다.
하지만 X는 1~N사이의 범위에 있는 값이므로 모순이 발생한다.
실제 예를 보자. N = 100, X = 70일 때, X의 A, B가 될 수 있는 조합은 (1, 70), (2, 35), (5, 14), (7, 10), (10, 7), (14, 5), (35, 2), (70, 1)이다. 보다시피 둘다 √N = 10보다 큰 값을 갖는 경우는 없다. 따라서 위에 언급했다시피 X의 부분인 A, B 둘 중 하나는 무조건 N의 제곱근보다 작거나 같아야 한다.
1 <= X <= N
X = A x B
if A, B > √N
then, A x B > N
False
실제로 우리가 N = 36을 A의 배수로 소수가 아닌 수를 지워나간다고 치자. A = 2일 때(X = A x B = 2 x 2, 2 x 3, 2 x 4, 2 x 5, ...)부터 차례대로 A의 배수를 차례대로 제거하다가 A가 √N = 6을 초과하고 나면, 다음 A의 값은 7인데 7 x 1은 소수니까 제외하고 7 x 2는 A = 2일때 제거됐고 7 x 3은 A = 3일때 제거됐다. 이처럼 N의 제곱근을 초과하고나면 나머지 값들은 이미 제거가 돼 있다. 따라서 배수를 제거할 때는 N의 제곱근까지만 제거해주면 소수만 남게 된다.
코드풀이
위의 설명을 바탕으로 파이썬으로 에라토스테네스의 체 코드를 구성했다. 다음은 100만까지의 수 중에서 소수의 총 개수를 구하는 코드다.
N = 10000000
sieve = [True for _ in range(N + 1)]
sieve[0] = sieve[1] = False
for i in range(2, int(N ** 0.5) + 1):
for j in range(i * 2, N + 1, i):
sieve[j] = False
print(sieve.count(True))- 0부터 N까지 소수임을 판별할 sieve 리스트를 만들어 준다. 코드가 끝난 뒤에 True로 남은 값들이 소수다.
- sieve[0], sieve[1]은 소수가 아니므로 False로 처리한다
- 첫번째 for문에서 2부터 N의 제곱근까지 i (위에서의 A)를 반복문을 돌린다.
- 지워지지 않은 가장 작은 수인 i * 1를 소수로 채택하고 두번째 for문은 i * 2부터 시작해 N까지 i씩 건너뛰며 i의 배수들인 sieve[j]를 False로 바꿔준다
이렇게 하면 기본적인 에라토스테네스의 체가 완성됐다. 하지만 몇가지 개선해야 할 점이 있다.
- 이미 제거된 값들인 4, 6, 8,...의 배수까지 체크 안해도 된다.
- i=10이라면 i * 2, i * 3, i * 4, ..., i * 9까지는 이전의 for문에서 이미 체크됐다.
이러한 부분을 개선한 코드는 다음과 같다.
N = 1000000
chae = [True for _ in range(N + 1)]
chae[0] = chae[1] = False
for i in range(2, int(N ** 0.5) + 1):
if chae[i] == True: # 🎃
for j in range(i * i, N + 1, i): # 🎃
chae[j] = False
print(chae.count(True))- chae[i]가 존재할 때만 for문을 돌리도록 개선했다.
- i * i부터 시작하도록 개선했다.
N이 1억일 때 시간 비교를 해보자
from datetime import datetime
# 개선 전 코드
N = 100000000
sieve = [True for _ in range(N + 1)]
sieve[0] = sieve[1] = False
past = datetime.now()
for i in range(2, int(N ** 0.5) + 1):
for j in range(i * 2, N + 1, i):
sieve[j] = False
print(sieve.count(True))
print(datetime.now() - past)
# 개선 후 코드
N = 100000000
chae = [True for _ in range(N + 1)]
chae[0] = chae[1] = False
past = datetime.now()
for i in range(2, int(N ** 0.5) + 1):
if chae[i] == True:
for j in range(i * i, N + 1, i):
chae[j] = False
print(chae.count(True))
print(datetime.now() - past)# 개선 전
5761455
0:00:33.039751
# 개선 후
5761455
0:00:09.753198
약 3배의 속도 개선이 있었다
개선 후 코드의 시간복잡도는 O(nloglogn)이다
'프로그래밍 > Computer Science' 카테고리의 다른 글
| [Overview] 01. Data Storage - (4) Data Compression (0) | 2023.07.14 |
|---|---|
| [Overview] 01. Data Storage - (3) The Binary System (0) | 2023.07.11 |
| [Overview] 01. Data Storage - (2) Main Memory (0) | 2023.07.11 |
| [Overview] 01. Data Storage - (1) Bit 그리고 Bit의 저장 (0) | 2023.07.09 |
| [알고리즘] 01. 정렬 알고리즘(Sorting Algorithm) (2) | 2023.03.29 |
